






目录
置顶证语………………( )
纲要……………………( )
上编 :大开篇(总论)
一、终极证明四色问题,路在何方?这是方法论提出的时代之问………………(39)
二、将无尽的外向证明,转换为大一统宏观调控下的可视证明………………(40)
三、确立“反求构图,正面证明”证略………………(47)
四、终极证明四色问题,其奧秘和关键在哪里?……(59)
五、终极证明四色问题的“双子塔”:转型演绎与终极构形图………………(61)
六、可控换色原理,是证明四色问题最基本的原理……(72)
七、结语
中编:登顶进行曲
一、概要………………(75)
二、登顶………………(78)
三、论证………………(91)
下编:辨异、四色可解(可染)定律及尾声
一、辨异…………………(97)
二、四色可解(可染)定律(101)
三、尾声………………(103)
附录:
一、《四色定理简证》(一证四色问题)…………()
二、《“海岛理论”与四色问题》(二证四色问题)……()
三、《五星图上“四色仙子”舞》(三证四色问题)……()
敢峰四色问题,是1850年英国的一位绘图员弗朗塞斯·古斯里(Guthrie)提岀的。其猜想是:绘制任何一张地图,只需要四种颜色,就可以使彼此相邻的各个区域,互相区别开来。当时谁也没想到,这个问题的数学证明,竟然成为一个半世纪中,世界最著名的数学三大难题之一。19世纪后期,律师兼数学家肯泊(Kempe),据平面图的欧拉公式,从渺无际涯的茫茫图海中,找到了证明四色问题的战略突破口:五轮构形图。这是一个里程碑式重大贡献。接着,青年数学家赫五德(Heawood)提出了有一个双环交叉线路的、四色难解的五轮图,由此,拉开了数学四色问题终极证明的大幕。(此前的证明,数学界已有定论,本文不再重述。)“突破口”论和“拉开了终极证明的大幕”论,是我对近现代四色问题证明的历史定位和定调。我的证明就是基于此展开的。为了便于读者和四色问题研究者,对本文的论述和作出的证明,大致先有一个简明的整体了解,把握全局,尽收精华和险要于眼底,特意在文前先写一个“置顶”证语和一个纲要性的话语网络。论文为塔式楼层结构,首先有一个大开篇。登临过程中,同一“胜景”在不同视角屡现,交相辉映。重要处不避重复。“横看成岭侧成峰,远近高低各不同”(前贤诗句),同时也为了减少读者前后查找的麻烦,还是多几个“瞭望”台和“探幽”处吧!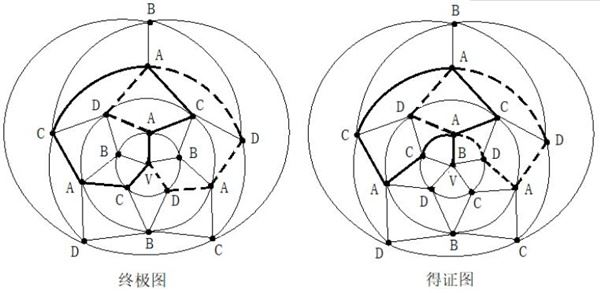
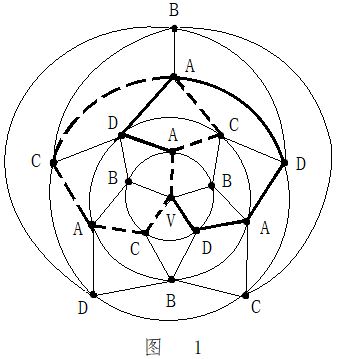
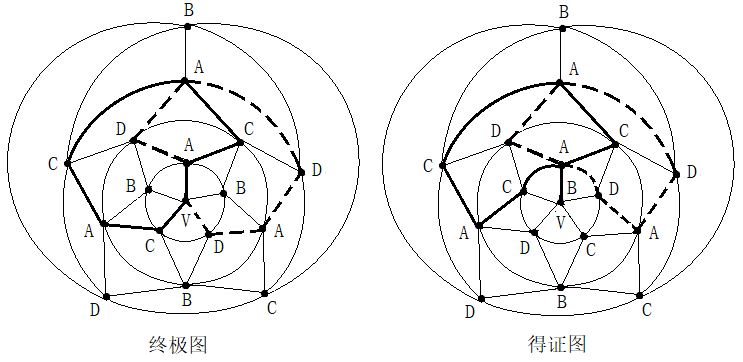
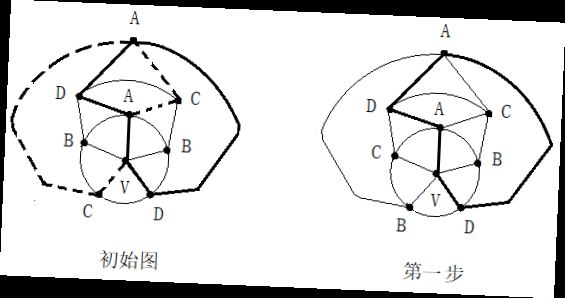
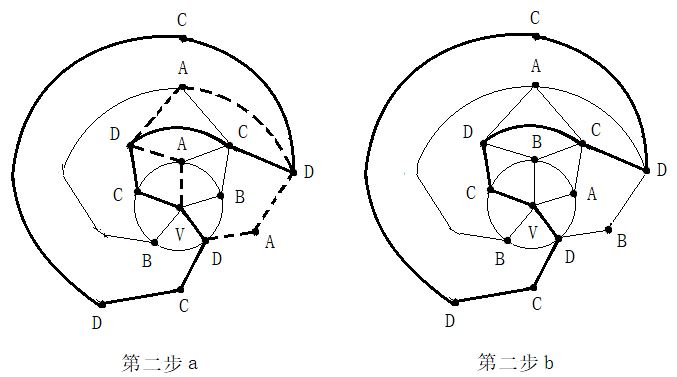
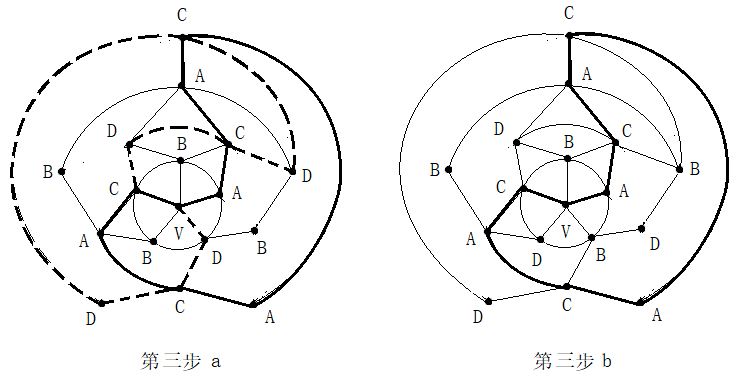
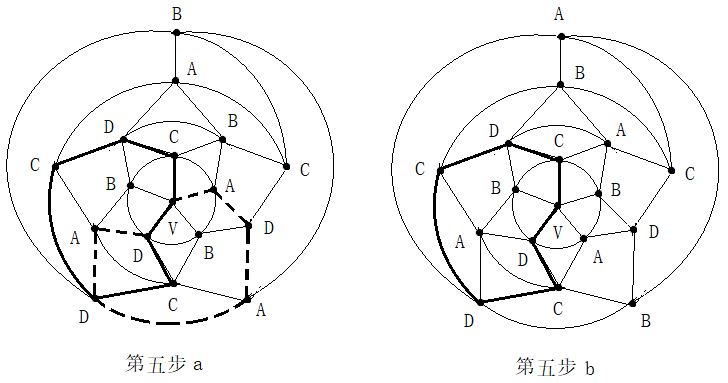
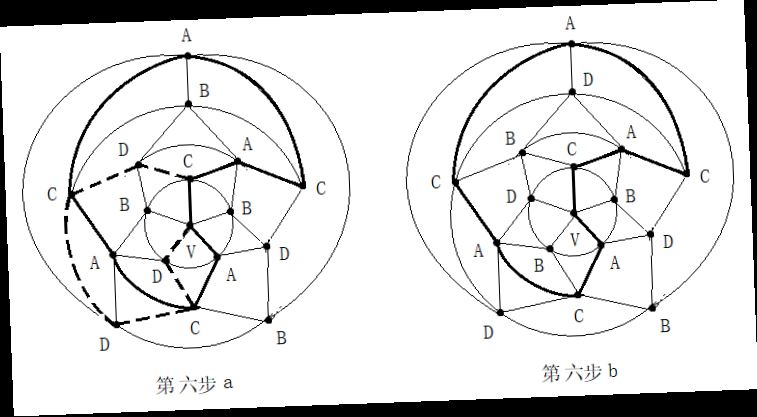
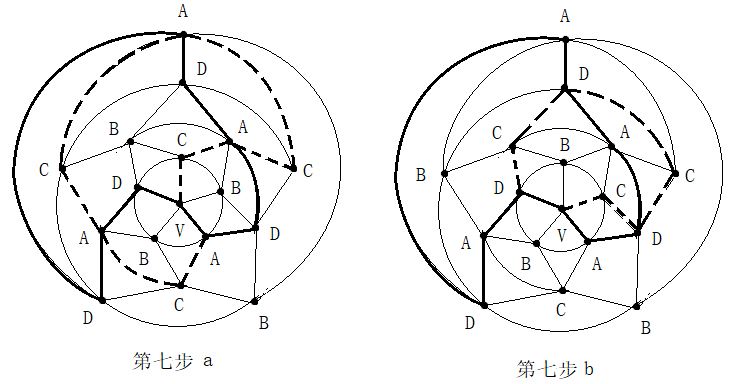
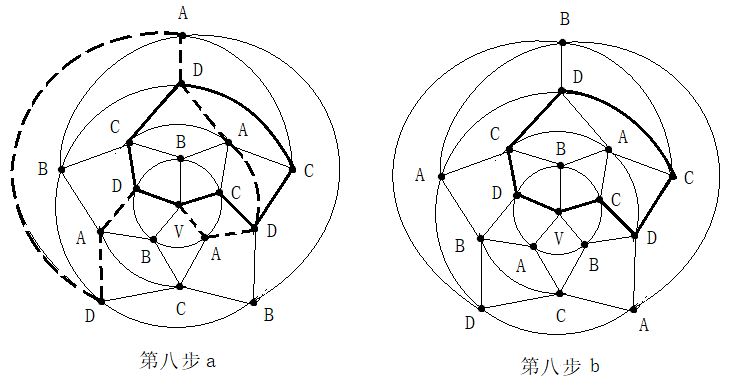
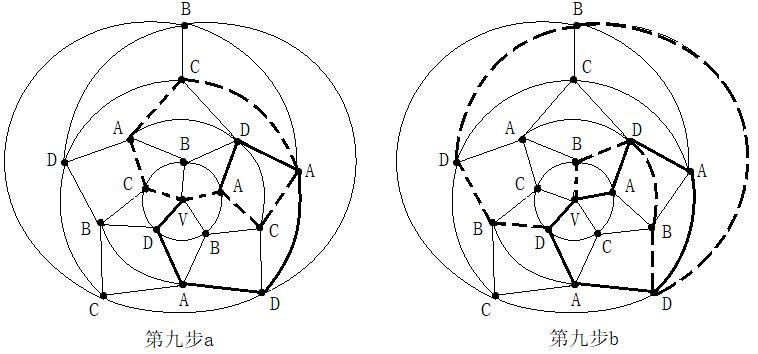
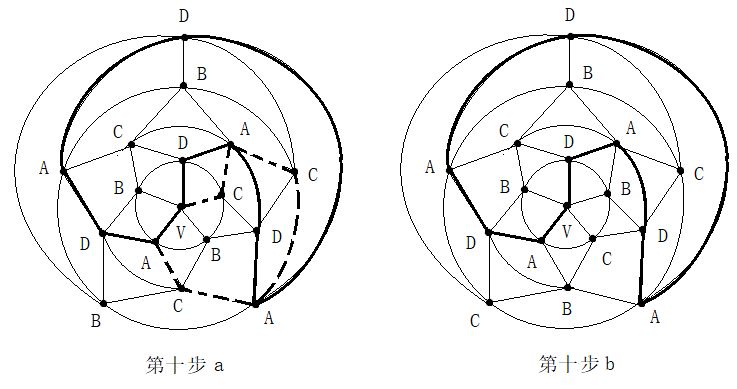
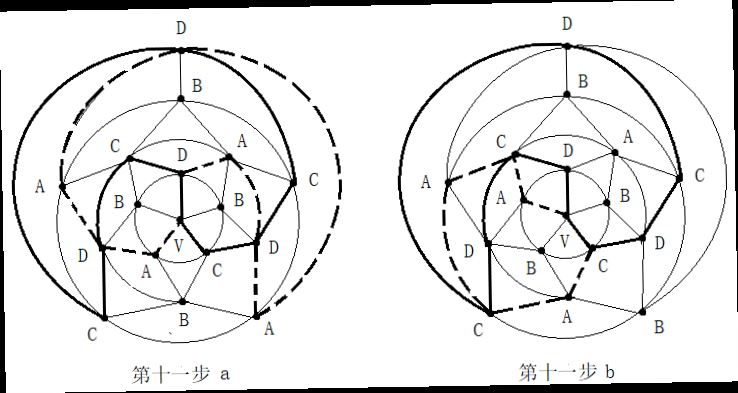
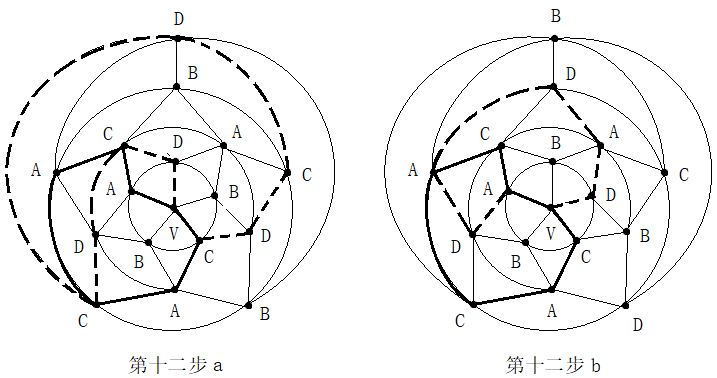
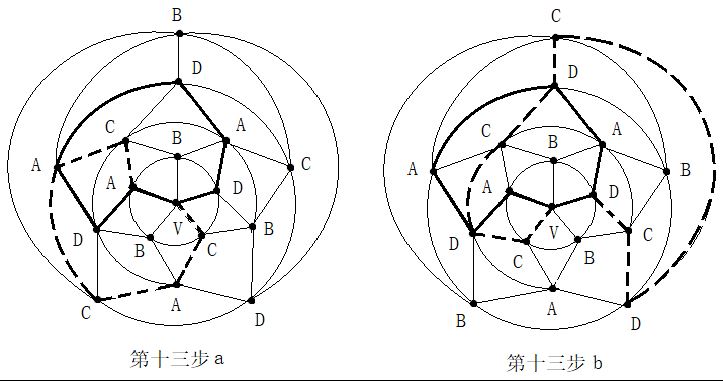
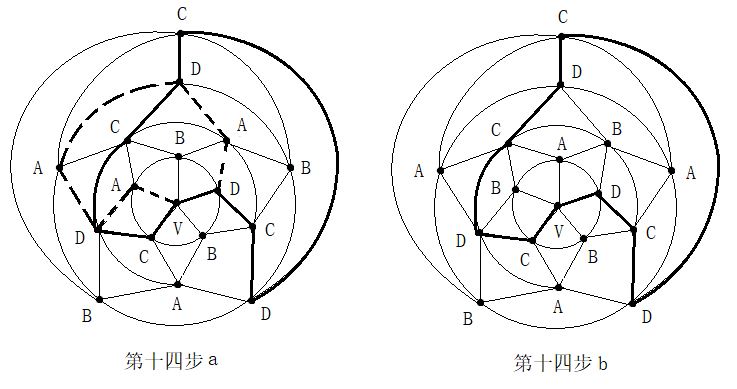
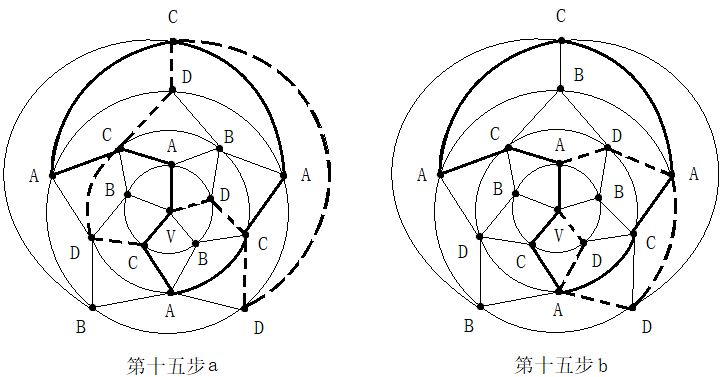
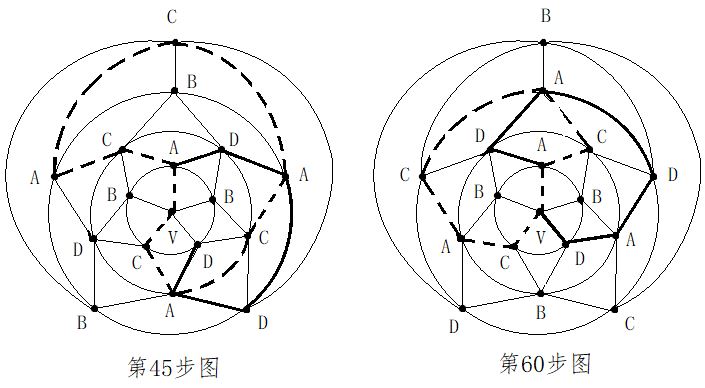
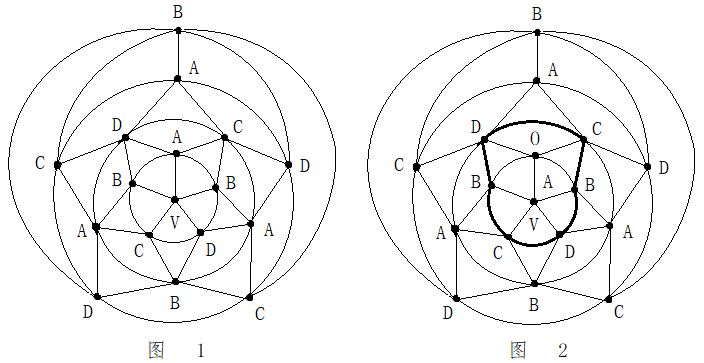
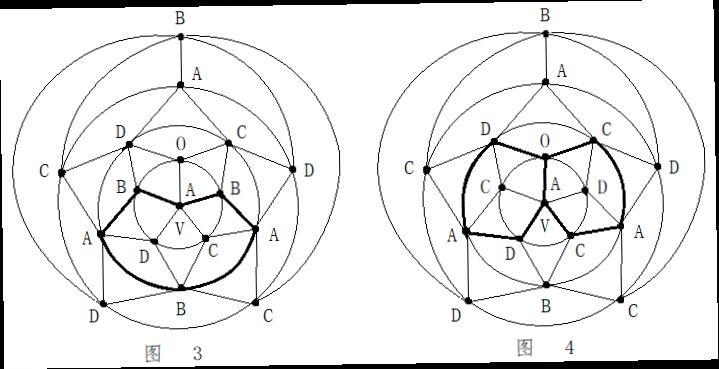
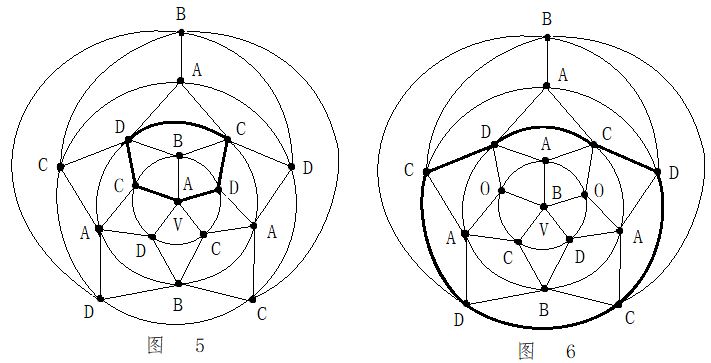
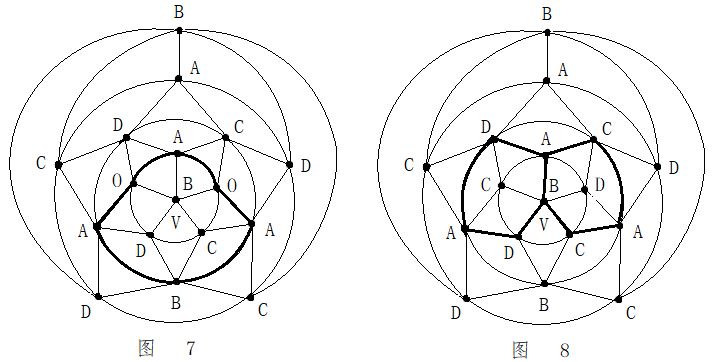
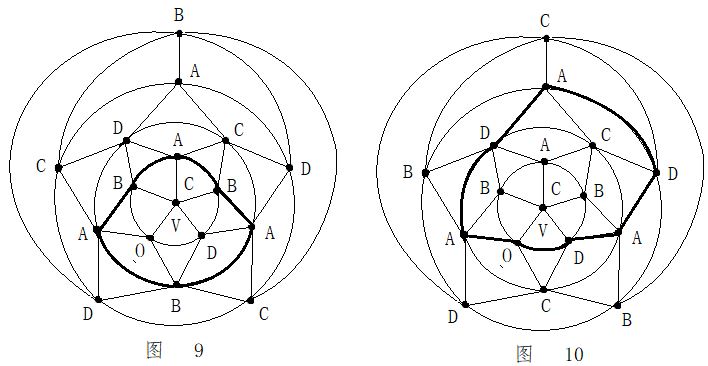
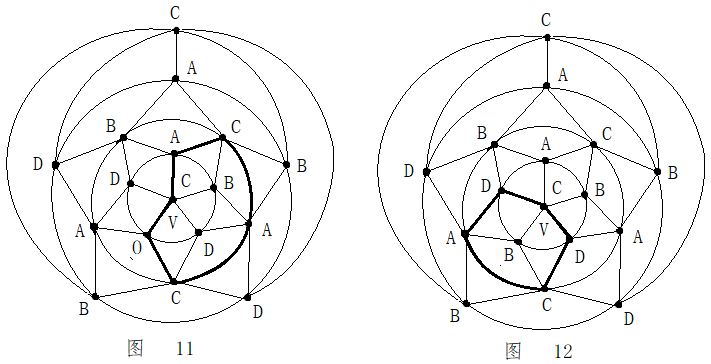
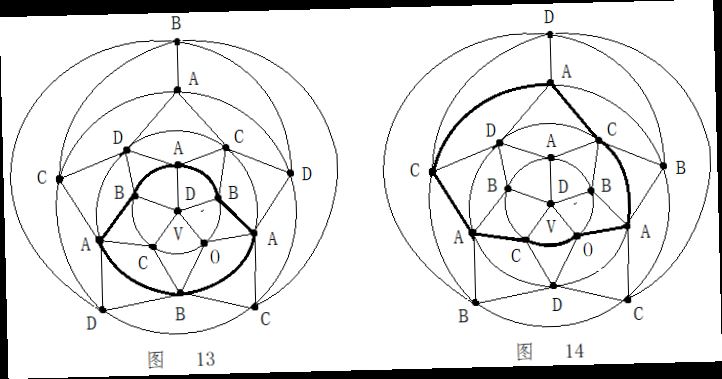 第二步:在五轮图沿新的A一C环外(通过0区),进行B与D二色互换,形成新的A一D环(通过0区)。见图14。
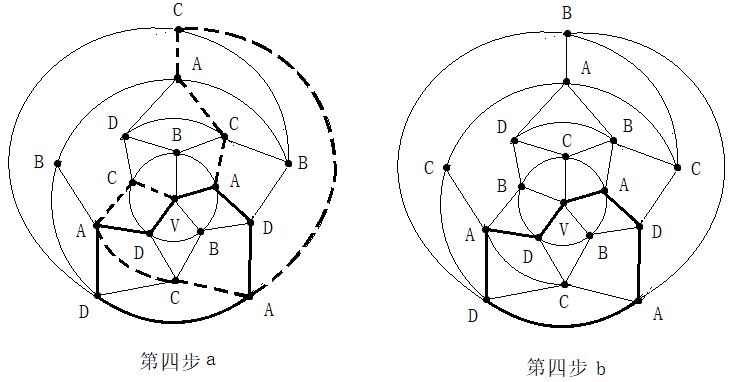
第二步:在五轮图沿新的A一C环外(通过0区),进行B与D二色互换,形成新的A一D环(通过0区)。见图14。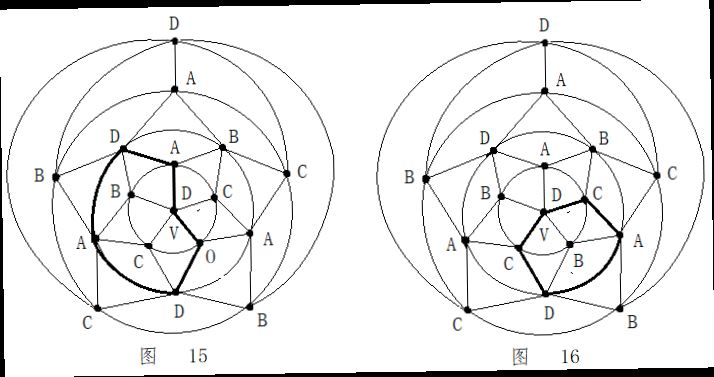 第四步:在C一D一C一D一A三色环中,将B色填入0区。见图16。
第四步:在C一D一C一D一A三色环中,将B色填入0区。见图16。
 据此,也可以"一槌定音",判定两者互不相干。
据此,也可以"一槌定音",判定两者互不相干。
马年春节重庆游火热 小语种导游成“香饽饽”
中新网重庆2月18日电 (梁钦卿 宋丹蕾)17日是大年初一,重庆市观音桥商圈内热闹非凡,一批来自东南亚的游客一边品尝着重庆特色美食,一边感受着浓浓的新春氛围。这批游客将在旅行社专属领队的带领下,开启为期5天的重庆旅程...(4896)人阅读时间:2026-02-18
2026年“新生活·新风尚·新年画”美术创作展示活动在江西抚州开幕
新闻视频 2026年2月11日,由中央宣传部文明实践局、文化和旅游部公共服务司、中国美术家协会、中国民间文艺家协会共同主办,文化和旅游部全国公共文化发展中心、中国...(22476)人阅读时间:2026-02-15
“折叠的时间”李庚艺术作品展在香港成功举办
新闻视频 2026年1月25日,由中国文化人物杂志社、北京慧和天语艺术空间、永添集团-ABLE STYLE形品艺术主办,李可染画院学术支持,中国美术家协会河山画会、首科院艺术科学...(20190)人阅读时间:2026-02-13
《太平年》带火“南宋CBD” 四方游客杭州赶“年市”
作者 林波 钱晨菲 “刚买了‘小九’钱弘俶在剧里爱吃的定胜糕,还是热乎的!”上海游客李玮以一块软糯香甜的糕点开启杭州之旅。 随着以五代十国吴越王钱弘俶&ld...(4534)人阅读时间:2026-02-13
陈茂波:香港培育新质生产力成果正逐渐显现
中新社香港2月8日电 香港特区政府财政司司长陈茂波8日发表网志称,国家“十五五”规划为香港下一阶段发展指明方向。香港在金融、贸易、创科等范畴都具有独特优势,有不少新领域、新内涵充满新机遇。 ...(4785)人阅读时间:2026-02-09